I remember the first time that I discovered the amazing feature called Common Table Expression (CTE), it was during my first read of Itzik Ben-Gan book (T-SQL Querying), maybe one of the most interesting feature together with Windows Functions. I know, I am a declared fan of CTE, but we can start defining a CTE as a sort of temporary result set and which exists only during the lifetime of the query.
This article is the first of a serie dedicated to recursive CTE and how we can use for solving some interesting scenarios. I would like to explain how we can utilize a CTE in a recursive way, it means that it can self-referencing, or even referenced multiple times in the same query. This capability of self-referencing opens a door of opportunities and scenarios for implementing a recursive query. I would like to mention a specific case that I had from customer requirement, it consisted in the implementation of a mechanism for “generating” a row a specific number of times based on a column which indicates us how many times the rows have to be repeated.
You have the next input information which has been adapted to be more didactic and easy to try:
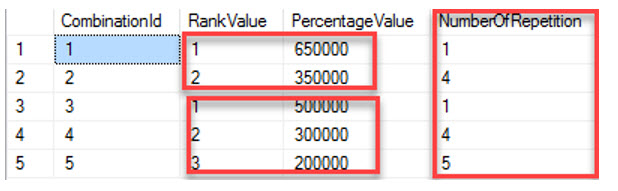
What it is the desired output, basically on the base of the number of repetition contained in the column NumberOfRepetition it should generate the CombinationId and the percentageValue rows the same number of times, for example for the CombinationId = 2 there are four repetitions which must have the PercentageValue equal to 350000.
For instance, the expected result for the first two rows should be:
I would like to define some key ideas about recursive CTE, the main structure of a recursive CTE is formed by the next elements: an anchor member, recursive member, and terminator. The next code shows a simple example:
WITH MyCTE AS     (SELECT 1 AS n -- anchor member UNION ALL SELECT n + 1 -- recursive member FROM   MyCTE WHERE  n < 100 -- terminator ) SELECT n FROM   MyCTE;We can define the anchor member as a query which is self-contained and executed only once, in the previous example was the initial point, later, we have the UNION ALL that indicate us the union of the anchor member with the result of the recursive query (the second section after UNION ALL). The key part which allows the recursivity is the reference to CTE name, in this case, MyCTE.
It is very important to notice that the reference of CTE name is basically the inmediate previous result, think in a process which is filling a kind of working table and consolidating the dataset, thus the recursive member is working aligns with the terminator for avoiding an infinite loop and allow it stops when there will not have more rows to processing, I mean, rows which not pass the filter defined by the terminator part.
The next code is built from scratch and you can see the logic behind it.
-- Set up the initial table for the testing purpose DECLARE @CombinationSeed AS TABLE ( [CombinationId] INT , [RankValue] INT , [PercentageValue] INT , [NumberOfRepetition] INT ); -- Populating the test table INSERT INTO @CombinationSeed ( [CombinationId] , [RankValue] , [PercentageValue] , [NumberOfRepetition] ) VALUES ( 1, 1, 650000, 1 ) , ( 2, 2, 350000, 3 ) , ( 3, 1, 500000, 1 ) , ( 4, 2, 300000, 4 ) , ( 5, 3, 200000, 5 ); -- Implementing the recursive CTE approach WITH MyCTE_Recursive AS ( SELECT * FROM @CombinationSeed UNION ALL SELECT MCR.CombinationId , MCR.RankValue , MCR.PercentageValue , MCR.NumberOfRepetition - 1 -- This operation is the key for filter it FROM MyCTE_Recursive AS MCR INNER JOIN @CombinationSeed AS MPP ON MCR.CombinationId = MPP.CombinationId WHERE MCR.NumberOfRepetition>1 ) SELECT MyCTE_Recursive.CombinationId , MyCTE_Recursive.PercentageValue FROM MyCTE_Recursive ORDER BY MyCTE_Recursive.CombinationId;
I would like to show you every stage that is processed in the previous query, in this way you could have a more clear picture.
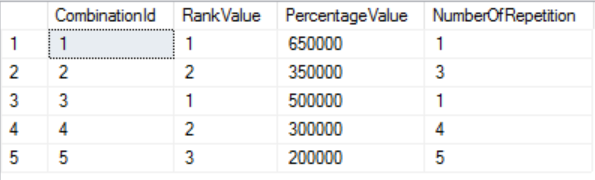
Iteration 1:
The first iteration consists of the processing of anchor member; in this case, it is the result of self-query with the next result:
Iteration 2:
As we have mentioned before, the anchor member result will be the seed that allows us to start the processing. The key part which yields recursion in this query is based on the reference to CTE, and knowing that initial dataset for the second iteration is the output of anchor member (above image), the second part of the query will join the CTE and the temporary table variable, it is equivalent to do:
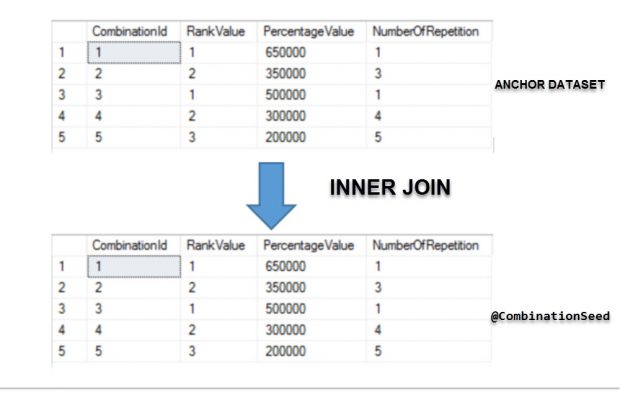
The result in this iteration will generate or clone one new row pre-existing, it is doing due to ON condition based on CombinationId column which is unique, being in this case the NumberOfRepetition the terminator, we should remind that in every iteration the NumberOfRepetition decreases in one until it is omitted because WHERE predicate set as condition it must be major than 1.
The rest of iterations follow the same pattern and internally the previous round is keeping dataset for using in the next iteration. The analysis of the Execution Plan built for recursive CTE is a subject out of scope, but I will address in a future blog. However, I would like to recommend you the next article of Grant Fichey where he talks about Spool operator: https://www.scarydba.com/2009/09/09/spools-in-execution-plans/
I hope that this blog would be useful for you and consider the use of CTE in some uncommon scenario like the exposed here.
More useful information about CTE and CTE Recursive can be found in the next links:
http://www.itprotoday.com/software-development/ctes-multiple-recursive-members
http://www.itprotoday.com/software-development/ctes-multiple-recursive-members-part-2
https://bit.ly/2ThTeGW

